前言
本文是基于《机器学习实战》中第4章《基于概率论的分类方法:朴素贝叶斯》的个人笔记兼回顾,代码与部分公式皆来自此书,在这里向无私的作者致以最真诚的敬意。
由于原书代码用Python2.7写成,下面的代码已用Python3重写了一遍,代码地址请点击这里。
贝叶斯决策理论
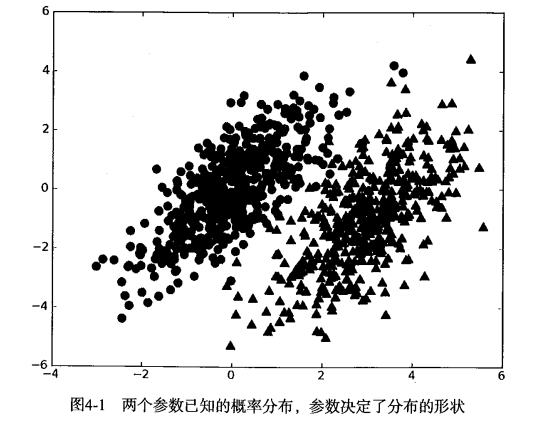
在上述数据集中,我们可以简单地用下面的规则来对数据集进行分类:
- 如果 p1(x,y) > p2(x,y) ,那么类别为1
- 如果 p2(x,y) > p1(x,y) ,那么类别为2
也就是说,我们会选择高概率对应的类别。这就是贝叶斯决策理论的核心思想,即选择具有最高概率的决策。
朴素贝叶斯分类方法
朴素贝叶斯之所以被称为“朴素”,是因为它假设将要被组合的各个概率之间是相互独立的。比如在下面的文档分类任务中,即可假设某个单词出现的概率与其他单词是不相关的,但实际上这个假设是不成立的。若不考虑假设的这种缺陷,朴素贝叶斯分类会是一种非常有效的文档分类方法。此外,朴素贝叶斯的另外一个假设是,每个特征都同等重要。
如果每个特征需要$N$个样本,那么对于10个特征需要$N^{10}$个样本,1000个特征需要$N^{1000}$个样本。可见,所需样本数会随着特征树木的增大而指数型增长。但是,如果假设特征之间相互独立,那么样本数可以从$N^{1000}$减少至$1000N$,这就大大降低了对数据量的要求。
贝叶斯定理
贝叶斯定理是一种对条件概率进行调换求解的方法,通常被写作:
示例1: 使用朴素贝叶斯进行文档分类(正常/侮辱性言论二分类)
在下面的示例中,我们将使用贝叶斯分类器对正常言论文档与侮辱性言论文档进行分类。
准备数据并创建词向量
1 | def loadDataSet(): |
应用贝叶斯公式
在这个示例中,我们将使用如下公式来计算概率。w表示一个词向量,即[0,1,0,1,1,0...],表示该文档中单词在词汇表中的出现情况,w的长度与词汇表相同。
我们将按如下步骤计算概率(观察上式,其实对于一个文档来说只要计算分子就行了):
- 计算$P(c_i)$,将类别
i(正常言论/侮辱性言论)中文档数除以总文档数即可。 - 计算$P(w|c_i)$,根据朴素贝叶斯假设,将
w展开为一个个的独立特征,可以写作$P(w_0,w_1,w_2…w_n|c_i)$。假设所有单词都互相独立,则可以用$P(w_0|c_i)P(w_1|c_i)P(w_2|c_i)…P(w_n|c_i)$来计算$P(w|c_i)$。
程序实现
下面就可以用代码实现上述公式了。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28def _trainNB0(trainMatrix, trainCategory):
"""
朴素贝叶斯原版
"""
numTrainDocs = len(trainMatrix) # 文件数
numWords = len(trainMatrix[0]) # 单词数
# 侮辱性文件的出现概率,即trainCategory中所有的1的个数
pAbusive = sum(trainCategory) / float(numTrainDocs)
# 单词出现次数列表
p0Num = np.zeros(numWords) # [0,0,0,.....]
p1Num = np.zeros(numWords) # [0,0,0,.....]
# 整个数据集单词出现总数
p0Denom = 0.0
p1Denom = 0.0
for i in range(numTrainDocs):
if trainCategory[i] == 1:
# 如果是侮辱性言论,对侮辱性言论的向量进行加和
p1Num += trainMatrix[i] #[0,1,1,....] + [0,1,1,....]->[0,2,2,...]
# 对向量中的所有元素进行求和,也就是计算所有侮辱性言论中出现的单词总数
p1Denom += sum(trainMatrix[i])
else:
# 不是侮辱性言论
p0Num += trainMatrix[i]
p0Denom += sum(trainMatrix[i])
#每个元素做除法,得到1/0(侮辱性/正常)言论分类下每个单词出现概率
p1Vect = p1Num / p1Denom
p0Vect = p0Num / p0Denom
return p0Vect, p1Vect, pAbusive
由于公式中的连乘$P(w_0|c_i)P(w_1|c_i)P(w_2|c_i)…P(w_n|c_i)$,当出现一个概率值为0时,那么最后结果也会为0。对此,我们可以将所有词的出现概率预设为1/2。
此外,由于大部分的因子都很小,程序会下溢出(Python连乘许多很小的数时最后四舍五入会得到0)。对此,我们对乘积取自然对数。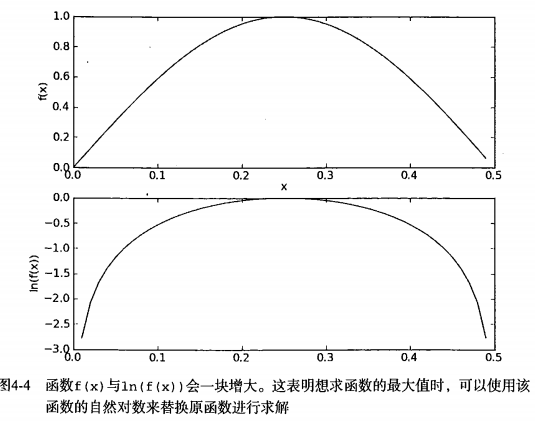
下面给出改进后的代码。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34def trainNB0(trainMatrix, trainCategory):
"""
朴素贝叶斯修正版,防止乘积为0与分母下溢出
"""
numTrainDocs = len(trainMatrix) # 文件数
numWords = len(trainMatrix[0]) # 单词数
# 侮辱性文件的出现概率,即trainCategory中所有的1的个数
pAbusive = sum(trainCategory) / float(numTrainDocs)
# 单词出现次数列表
# p0Num = np.zeros(numWords) # [0,0,0,.....]
# p1Num = np.zeros(numWords) # [0,0,0,.....]
p0Num = np.ones(numWords) # [0,0,0,.....]
p1Num = np.ones(numWords) # [0,0,0,.....]
# 整个数据集单词出现总数
# p0Denom = 0.0
# p1Denom = 0.0
p0Denom = 2.0
p1Denom = 2.0
for i in range(numTrainDocs):
if trainCategory[i] == 1:
# 如果是侮辱性言论,对侮辱性言论的向量进行加和
p1Num += trainMatrix[i] #[0,1,1,....] + [0,1,1,....]->[0,2,2,...]
# 对向量中的所有元素进行求和,也就是计算所有侮辱性言论中出现的单词总数
p1Denom += sum(trainMatrix[i])
else:
# 不是侮辱性言论
p0Num += trainMatrix[i]
p0Denom += sum(trainMatrix[i])
#每个元素做除法,得到1/0(侮辱性/正常)言论分类下每个单词出现概率
# p1Vect = p1Num / p1Denom
# p0Vect = p0Num / p0Denom
p1Vect = np.log(p1Num / p1Denom)
p0Vect = np.log(p0Num / p0Denom)
return p0Vect, p1Vect, pAbusive
现在就可以构建完整的分类器了。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1):
"""
朴素贝叶斯分类器
乘法转加法:
P(w1|c)*P(w2|c)....P(wn|c)P(c) -> log(P(w1|c))+log(P(w2|c))+....+log(P(wn|c))+log(P(c))
"""
p1 = sum(vec2Classify * p1Vec) + np.log(pClass1)
p0 = sum(vec2Classify * p0Vec) + np.log(1.0 - pClass1)
if p1 > p0:
return 1
else:
return 0
def runNB(testEntry, myVocabList, p0V, p1V, pAb):
thisDoc = np.array(setOfWords2Vec(myVocabList, testEntry))
classified_result = classifyNB(thisDoc, p0V, p1V, pAb)
if classified_result == 0:
print(testEntry,'classified as: {}'.format(classified_result),'正常言论')
else:
print(testEntry,'classified as: {}'.format(classified_result),'侮辱性言论')
测试结果
下面用两条言论['love', 'my', 'dalmation'],['stupid', 'garbage']测试一下分类效果:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18def testingNB():
"""
测试NB分类器
"""
listOPosts, listClasses = loadDataSet()
myVocabList = createVocabList(listOPosts)
trainMat = []
for postinDoc in listOPosts:
trainMat.append(setOfWords2Vec(myVocabList, postinDoc))
p0V, p1V, pAb = trainNB0(np.array(trainMat), np.array(listClasses))
# 测试言论1
testEntry = ['love', 'my', 'dalmation']
runNB(testEntry,myVocabList,p0V, p1V, pAb)
# 测试言论2
testEntry = ['stupid', 'garbage']
runNB(testEntry,myVocabList,p0V, p1V, pAb)
结果:1
2
3>>> testNB()
>>> ['love', 'my', 'dalmation'] classified as: 0 正常言论
['stupid', 'garbage'] classified as: 1 侮辱性言论
示例2: 使用朴素贝叶斯过滤垃圾邮件
词集模型与词袋模型
在这个示例中,我们将更进一步对垃圾邮件进行分类。上个示例中将每个词的出现与否作为一个特征,这可以被描述为词集模型(set-of-words model)。如果一个词在文档中出现不止一次,这可能意味着包含该词是否出现在文档中所不能表达的某种信息,这种方法被称为词袋模型(bag-of-words model)。在词袋中,每个单词可以出现多次,而在词集中,每个词只能出现一次。1
2
3
4
5
6
7
8
9
10
11
12
13def bagOfWords2VecMN(vocabList, inputSet):
"""
词袋模型(bag-of-words model)
与词集模型的不同在于每次累加单词出现次数
"""
returnVec = [0] * len(vocabList)
for word in inputSet:
if word in vocabList:
returnVec[vocabList.index(word)] += 1
else:
# print('the word: {} is not in my vocabulary'.format(word))
pass
return returnVec # returnVec = [0,1,0,1...]
准备数据并切分文本
数据集分为spam与ham,各包含25条邮件。内容如如下:1
2
3
4
5
6
7
8Hi Peter,
With Jose out of town, do you want to
meet once in a while to keep things
going and do some interesting stuff?
Let me know
Eugene
下面将邮件切分为单词1
2
3
4
5
6def textParse(bigString):
"""
切分文本,去掉标点符号并转为小写
"""
listOfTokens = re.split(r'\W*', bigString) # 利用正则表达式来切分文本
return [tok.lower() for tok in listOfTokens if len(tok) > 0]
程序实现
我们将使用上文实现的trainNB0函数来实现对垃圾邮件分类。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39def spamTest():
"""
测试垃圾邮件NB分类器
"""
docList = []
classList = []
fullText = []
# email文件夹中只有25个邮件
for i in range(1, 26):
wordList = textParse(open('email/spam/{}.txt'.format(i)).read())
docList.append(wordList)
classList.append(1)
wordList = textParse(open('email/spam/{}.txt'.format(i)).read())
docList.append(wordList)
fullText.extend(wordList)
classList.append(0)
# 创建词汇表
vocabList = createVocabList(docList)
trainingSet = list(range(50))
testSet = []
# 随机取 10 个邮件用来测试
for i in range(10):
randIndex = int(np.random.uniform(0, len(trainingSet)))
testSet.append(trainingSet[randIndex])
del(trainingSet[randIndex])
trainMat = []
trainClasses = []
for docIndex in trainingSet:
trainMat.append(setOfWords2Vec(vocabList, docList[docIndex]))
trainClasses.append(classList[docIndex])
p0V, p1V, pSpam = trainNB0(trainMat, trainClasses)
errorCount = 0
for docIndex in testSet:
wordVector = setOfWords2Vec(vocabList, docList[docIndex])
if classifyNB(wordVector, p0V, p1V, pSpam) != classList[docIndex]:
errorCount += 1
print('the errorCount is: ',errorCount)
print('the testSet length is :',len(testSet))
print('the error rate is ',format(float(errorCount) / len(testSet)))
测试结果
1 | >>> spamTest() |
示例3: 使用朴素贝叶斯分类器从区域组织中获取关注热点
书中原文是使用朴素贝叶斯分类器从个人广告中获取区域倾向,但原书RSS源已失效,改为使用newyork与sfbay的groups(地区组织)源,我们将对newyork与sfbay的groups进行二分类。下面需要一个RSS库:FeedParser。1
2ny = feedparser.parse('https://newyork.craigslist.org/search/grp?format=rss')
sf = feedparser.parse('https://sfbay.craigslist.org/search/grp?format=rss')
计算高频词
由于一篇文章中诸如I,your,are,is,we,they,of,for这些没有太大意义的词汇出现次数非常之高,所以我们需要先找出这些高频词。1
2
3
4
5
6
7
8
9
10
11def calcMostFreq(vocabList,fullText):
"""
计算TopN高频词
"""
freqDict = {}
for token in vocabList:
# 统计每个词在文本中出现的次数
freqDict[token] = fullText.count(token)
# 根据每个词出现的次数从高到底对字典进行排序
sortedFreq = sorted(freqDict.items(),key = operator.itemgetter(1),reverse = True)
return sortedFreq[:10] # 返回出现次数最高的N个单词
导入停用词
为了方便,我们也可以导入常见的英文停用词。1
2
3
4
5
6
7def stopWords():
"""
导入停用词,来自http://www.ranks.nl/stopwords
"""
wordList = open('stopword/stopword.txt').read()
listOfTokens = re.split(r'\W*', wordList)
return listOfTokens
程序实现
该函数返回贝叶斯分类器对newyork与sfbay的groups文章错误率。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53def localWords(feed1,feed0):
"""
从RSS源获取数据,并测试朴素贝叶斯分类
"""
docList = []
classList = []
fullText = []
minLen = min(len(feed1['entries']),len(feed0['entries']))
for i in range(minLen):
wordList = textParse(feed1['entries'][i]['summary'])
docList.append(wordList)
fullText.extend(wordList)
classList.append(1)
wordList = textParse(feed0['entries'][i]['summary'])
docList.append(wordList)
fullText.extend(wordList)
classList.append(0)
vocabList = createVocabList(docList)
# 去除停用词
stopWordList = stopWords()
for stopWord in stopWordList:
if stopWord in vocabList:
vocabList.remove(stopWord)
"""
# 去除TopN高频词
top30Words = calcMostFreq(vocabList,fullText)
for pairW in top30Words:
if pairW[0] in vocabList:
vocabList.remove(pairW[0])
"""
trainingSet = list(range(2*minLen))
testSet = []
for i in range(5):
randIndex = int(np.random.uniform(0,len(trainingSet)))
testSet.append(trainingSet[randIndex])
del(trainingSet[randIndex])
trainMat = []
trainClasses = []
for docIndex in trainingSet:
trainMat.append(bagOfWords2VecMN(vocabList,docList[docIndex]))
trainClasses.append(classList[docIndex])
p0V,p1V,pSpam = trainNB0(np.array(trainMat),np.array(trainClasses))
errorCount = 0
for docIndex in testSet:
wordVector = bagOfWords2VecMN(vocabList,docList[docIndex])
if classifyNB(np.array(wordVector),p0V,p1V,pSpam) != classList[docIndex]:
errorCount += 1
print('the error rate is:',float(errorCount)/len(testSet))
return vocabList,p0V,p1V
该函数返回newyork与sfbay的Top20热点词。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20def getTopWords(ny,sf):
"""
取出前20个热点词
"""
vocabList,p0V,p1V = localWords(ny,sf)
topNY = []
topSF = []
for i in range(len(p0V)):
if p0V[i]>-6.0:topSF.append((vocabList[i],p0V[i]))
if p1V[i]>-6.0:topNY.append((vocabList[i],p1V[i]))
sortedSF = sorted(topSF,key = lambda pair:pair[1],reverse = True)
print("SF**SF**SF**SF**SF**SF**SF**SF**SF**SF**SF**SF**SF**SF**")
for item in sortedSF[0:20]:
print(item[0])
sortedNY = sorted(topNY,key = lambda pair:pair[1],reverse = True)
print("NY**NY**NY**NY**NY**NY**NY**NY**NY**NY**NY**NY**NY**NY**")
for item in sortedNY[0:20]:
print(item[0])
测试结果
1 | def topwordsTest(): |
可以看出旧金山的groups更关注于life、club、players等,纽约的groups则更关注于divorce、court等,还是挺有意思的。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48>>> topwordsTest()
>>> the error rate is: 0.2
SF**SF**SF**SF**SF**SF**SF**SF**SF**SF**SF**SF**SF**SF**
life
group
looking
people
meet
join
help
years
working
morgan
every
problems
get
want
support
club
players
relationships
month
seeking
NY**NY**NY**NY**NY**NY**NY**NY**NY**NY**NY**NY**NY**NY**
divorce
court
island
ganesh
looking
new
necessary
york
city
help
8
plus
obtain
inexpensive
van
visits
file
weeks
look
prepare