Logistic回归

前言

本文是以《机器学习实战》、周志华《机器学习》、吴恩达《机器学习》Course公开课为基础的个人笔记。LaTeX大法好！

Sigmoid函数

定义：

$$y=\frac{1}{1+e^{-z}}$$

下图给出了Sigmoid函数在不同坐标尺度下的两条曲线图。当x为0时，Sigmoid函数值为0.5。显然，Sigmoid函数将前一级的线性输出映射到[0，1]之间的数值概率上。如果横坐标刻度足够大，Sigmoid函数看起来很像一个阶跃函数。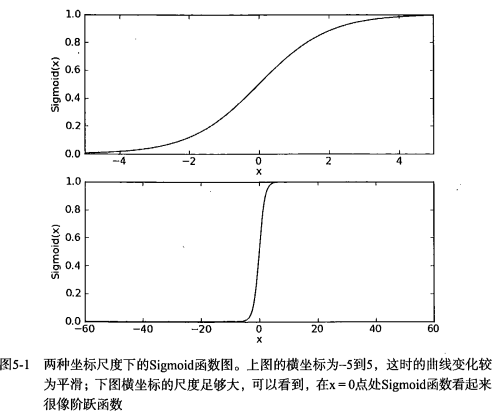


向量形式如下：

$$y=\frac{1}{1+e^{-\theta^{T}x}}\\$$

损失函数

不同于线性回归，如果我们简单地使用以下MSE(均方误差)作为loss函数，在Logistic回归中Sigmoid函数是一个非线性函数，这会使损失函数变得非凸，在应用梯度下降法时容易陷入局部最优解。

$$J(\theta)=\frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)}))-y^{(i)})^{2}$$

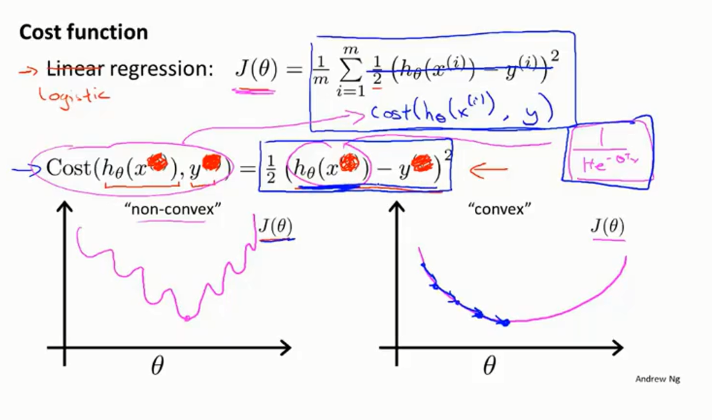
Andrew Ng在公开课中直接给出了如下的损失函数，但并没给出具体推导过程：

$$Cost(h_{\theta}(x),y) = \begin{cases} -log(h_{\theta}(x)) & \text {if y=1} \\ -log(1-h_{\theta}(x)) & \text{if y=0} \end{cases}$$ $$\begin{eqnarray*} J(\theta) &=& \frac{1}{2m}\sum_{i=1}^{m}Cost(h_\theta(x^{(i)}), y^{(i)})\\ &=&-\frac{1}{m} \displaystyle \sum_{i=1}^m \left(y^{(i)}\log (h_\theta (x^{(i)})) + (1 - y^{(i)})\log (1 - h_\theta(x^{(i)}))\right) \end{eqnarray*}$$

其中$Cost(h_{\theta}(x),y)=-log(h_\theta(x))$图像为: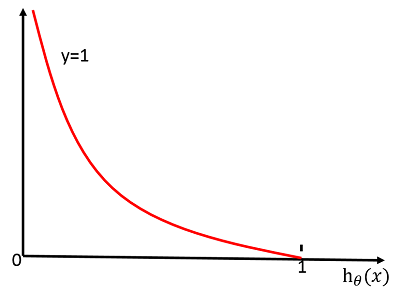

可以看出当$y=1$时，$Cost=0$，而当预测值$h_\theta(x)=0$时，我们将对损失函数施加一个很大的惩罚，即$Cost=\infty$。
当$Cost(h_{\theta}(x),y)=-log(1-h_\theta(x))$时同理。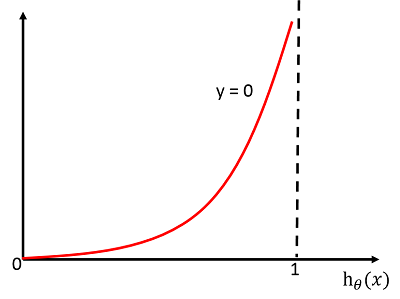

下面是推导过程：
对于输入$x$分类结果为类别$1$和类别$0$的概率分别为：

$$\begin{eqnarray*} h_{\theta}(x)&=&P(y=1|x;\theta)\\ 1-h_{\theta}(x)&=&P(y=0|x;\theta) \end{eqnarray*}$$

综合上述二式，可以写成：

$$P(y|x;\theta)=(h_{\theta}(x))^y\cdot (1-h_{\theta}(x))^{1-y}$$

构造似然函数：

$$L(\theta)=\prod_{i=1}^{m}P(y^{(i)}|x^{(i)};\theta) =\prod_{i=1}^{m}(h_{\theta}(x^{(i)}))^{y^{(i)}}\cdot (1-(h_{\theta}(x^{(i)}))^{1-y^{(i)}}$$

对似然函数取对数：

$$\begin{eqnarray*} logL(\theta)&=&log(\prod_{i=1}^{m}(h_{\theta}(x^{(i)}))^{y^{(i)}}\cdot (1-(h_{\theta}(x^{(i)}))^{1-y^{(i)}})\\ &=&\sum_{i=1}^m\left(y^{(i)}log \ h_{\theta}(x^{(i)})+(1-y^{(i)})log\ (1-h_{\theta}(x^{(i)}))\right) \end{eqnarray*}$$

取负数求均值即可得到损失函数：

$$\begin{eqnarray*} J(\theta) &=& -\frac{1}{m}logL(\theta)\\ &=&-\frac{1}{m}\sum_{i=1}^m\left(y^{(i)}log \ h_{\theta}(x^{(i)})+(1-y^{(i)})log\ (1-h_{\theta}(x^{(i)}))\right) \end{eqnarray*}$$

其中:

$$h_\theta (x^{(i)}) = \frac{1}{1+e^{-\theta^\mathrm {T} x}}$$

应用梯度下降法

Sigmoid函数求导过程如下，这一步将在下面求解梯度时用到：

$$\begin{align} y' & =\left(\frac{1}{1+e^{-z}} \right)'\\ & = \frac{e^{-z}}{(1+e^{-z})^2} \\ & = \frac{1+e^{-z}-1}{(1+e^{-z})^2} \\ & = \frac{1}{(1+e^{-z})} - \frac{1}{(1+e^{-z})^2}\\ & = \frac{1}{(1+e^{-z})} \cdot \left (1 - \frac{1}{(1+e^{-z})} \right) \\ & = y(1-y) \end{align}$$

向量形式：

$$\begin{eqnarray*} h_\theta (x){}' &=& \left( \frac{1}{1+e^{-\theta^\mathrm {T} x}} \right){}'\\ &=&-\frac{(1+e^{-\theta^\mathrm {T} x}){}'}{(1+e^{-\theta^\mathrm {T} x})^{2}} \\&=& \frac{e^{-\theta^\mathrm {T}x}(\theta^\mathrm {T} x){}'}{(1+e^{-\theta^\mathrm {T} x})^{2}} \\&=& \left(\frac{1}{1+e^{-\theta^\mathrm{T}x}}(1-\frac{1}{1+e^{-\theta^\mathrm{T}x}})\right)\cdot(\theta^\mathrm{T}x){}' \\&=& h_\theta(x)(1-h_\theta(x))(\theta^\mathrm{T}x){}' \end{eqnarray*}$$

梯度下降法的一般形式如下，α为学习率：

$$\theta_j := \theta_j - \alpha \dfrac{\partial}{\partial \theta_j}J(\theta)$$

求偏导过程如下，比较麻烦，一步步来吧：

$$\begin{eqnarray*} \dfrac{\partial}{\partial \theta_j}J(\theta)&=&-\frac{1}{m}\sum_{i=1}^m\left(y^{(i)}log \ h_{\theta}(x^{(i)})+(1-y^{(i)})log\ (1-h_{\theta}(x^{(i)}))\right)'\\ &=&-\frac{1}{m}\sum_{i=1}^m\left(y^{(i)}\frac{1}{h_\theta(x^{(i)})}h_\theta^\prime(x^{(i)})-(1-y^{(i)})\frac{1}{1-h_\theta(x^{(i)})}h_\theta^\prime(x^{(i)})\right)\\ &=&-\frac{1}{m}\sum_{i=1}^m\left(y^{(i)}(1-h_\theta({x^{(i)}})) \cdot(\theta^\mathrm{T}x){}'- (1-y^{(i)})\cdot(h_\theta(x^{(i)}))\cdot(\theta^\mathrm{T}x){}'\right)\\ &=&-\frac{1}{m}\sum_{i=1}^m\left(y^{(i)}-h_\theta(x^{(i)})\right)\cdot(\theta^{T}x)'\\ &=&\frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)} \end{eqnarray*}$$

其中$(\theta^\mathrm{T}x){}’$为对第$j$个$\theta$求偏导，即$x_j^{(i)}$

由于α与$\frac{1}{m}$连乘得到还是常量，将$\frac{1}{m}$省略，最后得到梯度更新公式为：

$$\theta_j := \theta_j - \alpha \sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}$$

至此，推导完成。