前言
k-近邻(kNN,k-NearestNeighbor)是最简单有效的一种用于分类与回归的算法之一。所谓k最近邻,就是k个最近的邻居的意思,即每个样本都可以用它最接近的k个邻居来代表。
k值选择、距离度量、决策规则是k近邻算法的三个基本要素。
k-近邻做回归和分类的主要区别在于最后做预测时候的决策方式不同。当做分类预测时,一般是选择多数表决法,即训练集里和预测的样本特征最近的k个样本,预测为里面有最多类别数的类别。而做回归时,一般是选择平均法,即最近的k个样本的样本输出的平均值作为回归预测值。
对于原始kNN计算量大的缺点,主要有KD树与球树两种改进算法。
参考:周志华-《机器学习》&Peter Harrington-《机器学习实战》
Mohamad Dolatshah, Ali Hadian, Behrouz Minaei-Bidgoli, “Ball-tree: Efficient spatial indexing for constrained nearest-neighbor search in metric spaces”, ArXiv e-prints, Nov 2015.
k值选择
k值越小,偏差越小、方差越大,容易过拟合,不抗噪声。
k值越大,偏差越大、方差越小,容易欠拟合。
通常采用经验值或交叉验证选取合适的k值。
计算距离
欧式距离:
曼哈顿距离:
闵可夫斯基距离:
当$p=1$时,就是曼哈顿距离;当$p=2$时,就是欧氏距离。
原始kNN(Brute Force)
原始的kNN算法在找近邻时采取的是Brute Force算法,暴力对所有训练集样本进行搜索,有两个明显的缺点:
1.需要存储全部训练集
2.计算量太大
一种有效的改进方法是事先将训练集按近邻关系分解成组,算出每组质心的位置,以质心作为代表点,和未知样本计算距离,选出距离最近的一个或若干个组,再在组的范围内应用原始的kNN算法。由于并不是将未知样本与所有样本计算距离,故该改进算法可以减少计算量,但并不能减少存储量。
实现k-近邻法时,主要考虑的问题是如何对训练数据进行快速k近邻搜索,为了减少计算量,可以考虑使用特殊的结构存储训练数据,以减小计算距离的次数,比如引入树结构。
KD树
KD树(K-dimension tree)是一种对k维空间中的实例点进行存储以便对其进行快速检索的树形数据结构。KD树是是一种二叉树,表示对k维空间的一个划分,构造KD树相当于不断地用垂直于坐标轴的超平面将K维空间切分,构成一系列的K维超矩形区域。KD树的每个结点对应于一个K维超矩形区域。利用KD树可以省去对大部分数据点的搜索,从而减少搜索的计算量。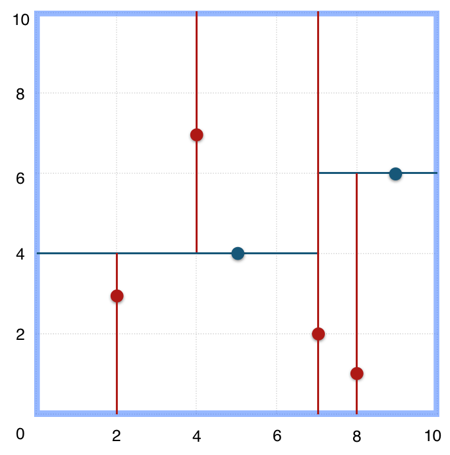
下面是三维空间下KD树的构建及空间划分过程。
首先,边框为红色的竖直平面将整个空间划分为两部分,此两部分又分别被边框为绿色的水平平面划分为上下两部分。最后此4个子空间又分别被边框为蓝色的竖直平面分割为两部分,变为8个子空间,此8个子空间即为叶子节点。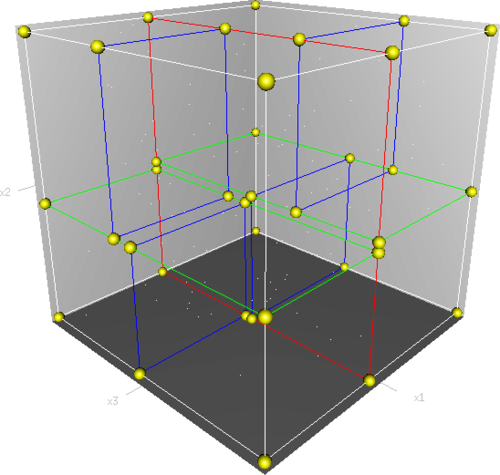
KD树的建立
KD树建树采用的是从$m$个样本的$n$维特征中,分别计算$n$个特征的取值的方差,用方差最大的第$k$维特征$n_k$来作为根节点。对于这个特征,选择特征$n_k$的取值的中位数$n_kv$对应的样本作为划分点,对于所有第$k$维特征的取值小于$n_kv$的样本,划入左子树,对于第$k$维特征的取值大于等于$n_kv$的样本,划入右子树,对于左子树和右子树,采用和刚才同样的办法来找方差最大的特征来做根节点,递归生成KD树。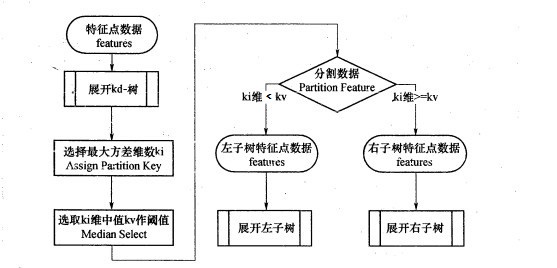
比如现在有$6$个二维样本,$(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)$,构建KD树的具体步骤为:
- 找到划分的特征。$6$个数据点在$x$,$y$维度上的数据方差分别为$6.97$,$5.37$,所以在$x$轴上方差更大,用第$1$维特征建树。
- 确定划分点$(7,2)$。根据$x$维上的值将数据排序,$6$个数据的中值为$7$,所以划分点的数据是$(7,2)$。这样该节点的分割超平面就是通过$(7,2)$并垂直于划分点维度的直线$x=7$;
- 确定左子空间和右子空间。分割超平面$x=7$将整个空间分为两部分:$x<=7$的部分为左子空间,包含$3$个节点${(2,3),(5,4),(4,7)}$;另一部分为右子空间,包含$2$个节点${(9,6),(8,1)}$。
- 构建$(7,2)$节点的左子树时,点集合$(2,3),(4,7),(5,4)$。$3$个数据点在$x$,$y$维度上的数据方差分别为$2.33$,$4.33$,此时的切分维度为$y$。中值为$(5,4)$作为分割平面,$(2,3)$挂在其左子树,$(4,7)$挂在其右子树。
- 构建$(7,2)$节点的左子树同理。
最后得到的KD树如下: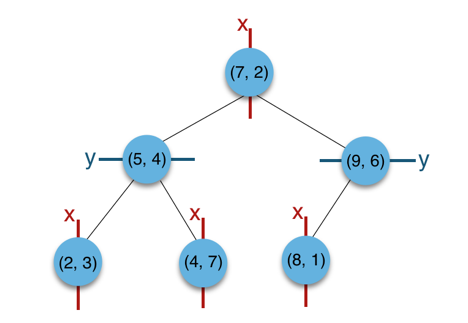
最近邻搜索
以上述建立的KD树来寻找$(2,4.5)$的最近邻。
- 二叉搜索:首先从根节点$(7,2)$出发,由于目标点$x=2 < 7$,进入左子树$(5,4)$。由于目标点$y=4.5>4$,进入右子树$(4,7)$,形成搜索路径${(7,2)-(5,4)-(4,7)}$。
- 回溯:节点$(4,7)$与目标查找点距离为$3.202$,回溯到父节点$(5,4)$与目标查找点之间距离为$3.041$,所以$(5,4)$为查询点的最近邻。以目标点(2,4.5)为圆心,以3.041为半径作圆。
- 更新最近邻:该圆和$y = 4$超平面交割,所以需要进入$(5,4)$左子树进行查找。回溯至节点$(2,3)$,$(2,4.5)$到$(2,3)$的距离比到$(5,4)$要近,所以最近邻点更新为$(2,3)$,最近距离更新为$1.5$。回溯至$(7,2)$,以$(2,4.5)$为圆心,$1.5$为半径作圆,发现并不和$x = 7$分割超平面交割,至此搜索路径回溯完成,完成更新最近邻操作,返回最近邻点$(2,3)$。
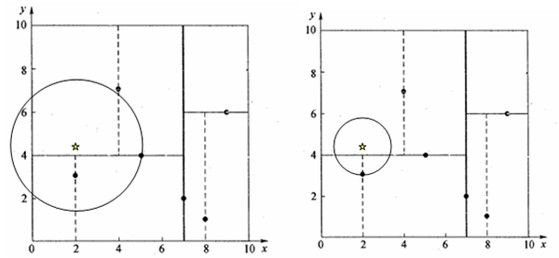
根据KD树搜索最近邻的方法,可以得到第一个最近邻样本点,将它置为已选。然后忽略置为已选的样本,重新选择最近邻,这样运行k次,就可以得到k个最近邻。
如果样本点是随机分布的,KD树搜索的平均计算复杂度是$O(logN)$,这里$N$是训练实例数。KD树更适用于训练实例数远大于空间维数时的k近邻搜索。当空间维数接近训练实例数时,它的效率会迅速下降,几乎接近线性扫描。
球树
KD树算法能够提高kNN搜索效率,但在某些时候效率并不高,比如处理不均匀分布的数据集时。
如下图所示,如果黑色的实例点离目标点(星点)再远一点,那么虚线会像红线那样扩大,导致与左上方矩形的右下角相交。既然相交那就要检查左上方矩形,而实际上最近的点离目标点(星点)很近,检查左上方矩形区域已是多余。因此KD树把二维平面划分成矩形会带来无效搜索的问题。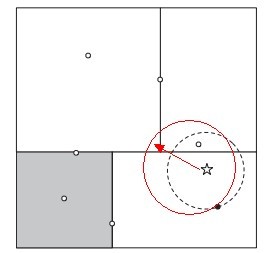
为了优化超矩形体导致的搜索效率的问题,引入球树。
球树的建立
球树的每个分割块都是超球体,而非KD树中的超矩形体。球树的构建过程如下:
- 构建超球体:超球体是可以包含所有样本的最小球体。
- 划分子超球体:从超球体中选择一个离超球体中心最远的点,然后选择第二个点离第一个点最远,将球中所有的点分配到离这两个聚类中心最近的一个。然后计算每个聚类的中心,以及聚类能够包含它所有数据点所需的最小半径,这样我们便得到两个子超球体,和KD树中的左右子树对应。
- 递归:对上述两个子超球体,递归执行步骤2,最终得到球树。
可以看出球树和KD树类似,主要区别在于球树得到的是节点样本组成的最小超球体,而KD得到的是节点样本组成的超矩形体,这个超球体要与对应的KD树的超矩形体小,这样在做最近邻搜索的时候,可以避免一些无效的搜索。
球树搜索最近邻
KD树在搜索路径优化时使用的是两点之间的距离来判断,而球树使用的是两边之和与第三边大小来判断,即$|x+y|\leq|x|+|y|$。
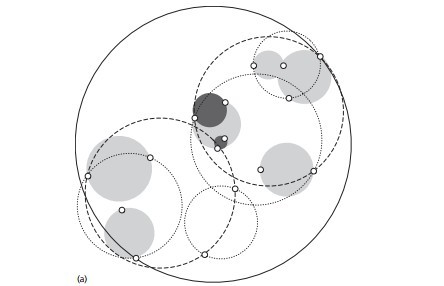
以下图为例搜索点$q$的半径为$r$内的最近邻,即满足$||q-x||\leq r$:
- 从根节点$q$开始从上至下递归遍历每个可能包含最终近邻的子空间$p_i$。
- 如果子空间的半径$radius{(p_i)}$与$r$之和小于$p_i$中心点$center(p_i)$到目标点$q$的距离,即$(radius(p_i)+r)\leq ||center(p_i)-q||$,接着在满足这样条件的子空间样本点内递归搜索满足$||q-x||\leq r$的点就是我们想要的最近邻点了。换句简单的话来说,对于目标空间$(q, r)$,所有被该超球体截断的子超球体内的所有子空间都将被遍历搜索。
- 由于子超球体$a$与$b$被$q$所截,而对于$a$与$b$内的子空间,$d,h,f$又被$q$所截,所以接下来就会在$d,h,f$内进行线性搜索。诸如$c,e,g$这些距离太远的子空间将被舍去。最后$[x_4,x_7]$就是最终得到最近邻。

球树中的每个结点对应一个圆,结点的数字表示该区域保含的观测点数,但不一定就是图中该区域囊括的点数,因为有重叠的情况,并且一个观测点只能属于一个区域。实际的球树结点保存圆心和半径。叶子结点保存它包含的观测点。
kNN实现手写数字分类
代码来自于《机器学习实战》第2章。
思路:
- 将每个32x32的图像数据转换成1x1024的向量
再将每个单列向量分别存入一个矩阵A中
矩阵A中每一列对应一张图片信息,m张图片对应的矩阵A的大小即为m*1024 - 将测试图片也转换为1x1024的向量后与矩阵A中每一列求欧式距离
将一一对应的距离存入一个数组中,取出距离数组中最小的k个训练集索引 - 索引出现次数最多的值就是预测数值
先处理图像数据1
2
3
4
5
6
7
8
9
10
11
12def img2vector(filename):
"""
将32*32的图像数据转换为1*1024的向量
循环读出文件的前32行,并将每行的前32个值存储在1*1024的numpy数组中
"""
returnVect = np.zeros((1,1024))
fr = open(filename)
for i in range(32):
lineStr = fr.readline()
for j in range(32):
returnVect[0,32*i+j] = int(lineStr[j])
return returnVect
构造分类器1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35def classify0(inX, dataSet, labels, k):
"""
利用k-近邻算法实现分类,采用欧式距离
inX: 用于分类的输入向量
dataSet: 训练集
labels: 标签向量
k: 选择最近邻数目
"""
dataSetSize = dataSet.shape[0]
# 将输入向量按行复制,与训练集相减得到差值
diffMat = np.tile(inX, (dataSetSize, 1)) - dataSet
# 各个差值分别平方
sqDiffMat = diffMat ** 2
# 按行对结果求和
sqDistances = sqDiffMat.sum(axis = 1)
# 再开方即可得到距离
distances = sqDistances ** 0.5
# argsort()方法将向量中每个元素进行排序,结果是元素的索引形成的向量
# 如argsort([1,3,2]) -> ([0,2,1])
sortedDistIndicies = distances.argsort()
classCount = {}
for i in range(k):
# 找到该样本的类型
voteIlabel = labels[sortedDistIndicies[i]]
# 在字典中将该类型+1
# 字典的get()方法
# 如:list.get(k,d)get相当于一条if...else...语句
# 参数k在字典中,字典将返回list[k]
# 如果参数k不在字典中则返回参数d,如果K在字典中则返回k对应的value值
classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1
# 字典的 items()方法,以列表返回可遍历的(key,value)元组
# sorted()中的第2个参数key=operator.itemgetter(1)表示按第2个元素进行排序
sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)
# 返回第0个tuple的第0个参数,由于是逆序排序所以返回的是出现次数最多的类型
return sortedClassCount[0][0]
测试分类器正确率1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30def handwritingClassTest():
"""
kNN手写数字识别测试
"""
# 导入训练集
hwLabels = []
trainingFileList = listdir('trainingDigits')
m = len(trainingFileList)
trainingMat = np.zeros((m, 1024))
for i in range(m):
fileNameStr = trainingFileList[i]
fileStr = fileNameStr.split('.')[0]
classNumStr = int(fileStr.split('_')[0])
hwLabels.append(classNumStr)
trainingMat[i, :] = img2vector('trainingDigits/%s' % fileNameStr)
# 导入测试集
testFileList = listdir('testDigits')
errorCount = 0.0
mTest = len(testFileList)
for i in range(mTest):
fileNameStr = testFileList[i]
fileStr = fileNameStr.split('.')[0]
classNumStr = int(fileStr.split('_')[0])
vectorUnderTest = img2vector('testDigits/%s' % fileNameStr)
classifierResult = classify0(vectorUnderTest, trainingMat, hwLabels, 3)
print("the classifier came back with: %d, the real answer is: %d" % (classifierResult, classNumStr))
if (classifierResult != classNumStr): errorCount += 1.0
print("\nthe total number of errors is: %d" % errorCount)
print("\nthe total correct rate is: %f" % (1-(errorCount / float(mTest))))
结果1
2
3
4
5
6
7
8...
the classifier came back with: 9, the real answer is: 9
the classifier came back with: 9, the real answer is: 9
the classifier came back with: 9, the real answer is: 9
the classifier came back with: 9, the real answer is: 9
the total number of errors is: 10
the total correct rate is: 0.989429
原始的kNN要做分类的话每张图片都得和每个训练集样本两两计算距离,如上述例子就是如此。时间复杂度就是O(M*N),虽然简单但是遇到数据集很大时会变得效率非常低,所以一般采用的是KD树或球树等改进型的kNN算法。scikit-learn中提供了kNN算法的三种实现,第一种是Brute Force(暴力)实现,第二种是KD树实现,第三种是球树实现。
kNN做回归比较简单,就是取k个近邻的平均值作为预测值,当有多个特征时可以为特征设置不同权重,或者给近点加大权重,远点减小权重,都可以提高预测准确率。