原论文
Yuxuan Liang, Songyu Ke, Junbo Zhang, Xiuwen Yi, Yu Zheng, “GeoMAN: Multi-level Attention Networks for Geo-sensory Time Series Prediction”, In International Joint Conference on Artificial Intelligence (IJCAI), 2018.
前言
之前都没关注过城市计算这个领域的问题,在搜索基于LSTM的PM2.5预测相关工作的时候偶然发现这篇来自AI顶会之一的paper,觉得这领域的一些内容也是十分具有前沿性与挑战性的,做的工作也非常有现实价值,此文作者是原微软亚洲研究院研究员、现京东金融集团副总裁、首席数据科学家郑宇。
据了解,京东的城市计算业务部已经部署了基于这个模型的自来水质预测系统,以期能够指导自来水工厂更科学地进行投氯消毒,保证居民饮用水质。还可以及时发现水管健康状态,并在第一时间进行维护、修理,为政府的城市建设决策提供参考。
摘要
城市中的传感器每天都源源不断不断地产生大量随着时间变化的数据,这些有着独立地理位置的传感器产生的时间序列数据之间往往存在着空间上的联系,论文将这些数据称为“地理传感器时间序列”(Geosensory Time Series)。如何对这些具有时空关联性的地理传感器时间序列数据进行预测是一个十分具有挑战性的问题。
这篇paper提出了一种GeoMAN(Multi-level Attention Network)结构的预测模型,该模型基于Encoder-Decoder结构,在时空数据预测问题上首次引入了多层注意力机制,对各传感器之间的动态时空关联性进行建模,并通过在Decoder阶段融合传感器对应的兴趣点(POI)信息、传感器ID和天气预报数据等外部因素显著提升了模型的性能。
该模型不仅在PM2.5预测上取得了成功,在自来水质预测上也有着同样的出色表现,是一个在地理传感器时间序列预测问题上通用的模型。
问题
预测时空序列数据的挑战性主要体现在以下两方面:一、动态的时空关联性;二、外部因素。
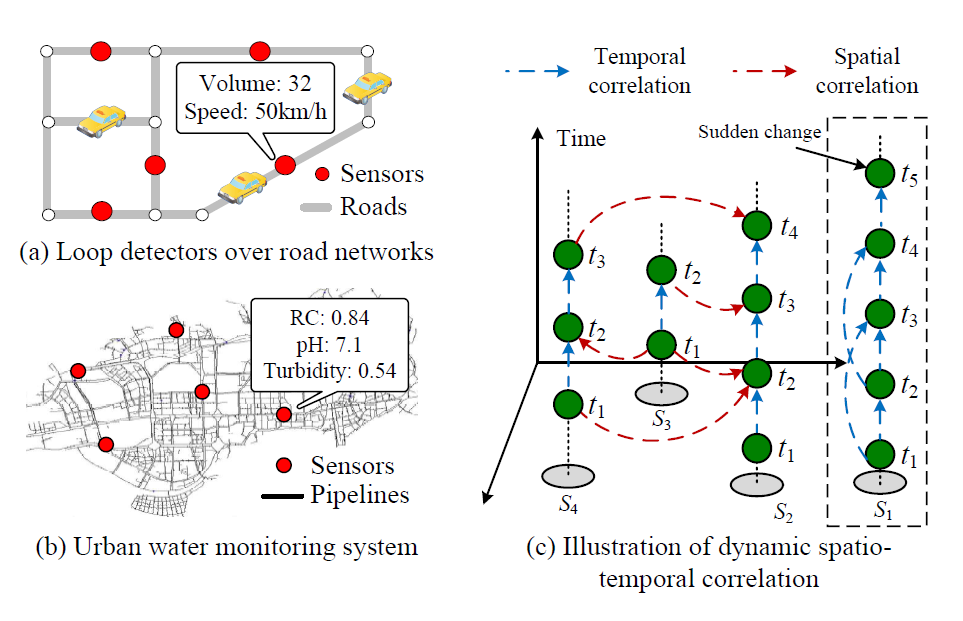
对于动态的时空关联性,体现在以下两方面。
一、不同传感器件复杂的空间关联性,如上图(c)中显示传感器间的空间相关性是随着时间高度动态变化的,并且地理位置是非线性相关的。
当对这些传感器进行成对的动态建模时,传统方法例如Koller与Friedman于2009年提出的概率图模型,由于其庞大的参数往往会花费十分昂贵的算力。
二、同种传感器内的动态相关性,地理传感器时序数据往往遵循着周期性模式,但有时候(例如突发极端天气、突发车流高峰、突发用水用电高峰等)传感器的数据会大幅波动,因此如何选取合适的时间间隔也是一个挑战。
对于外部因素,则体现在传感器数据会受到周围环境(强风强降水等)、所处时刻(高峰期与否)的影响。
模型
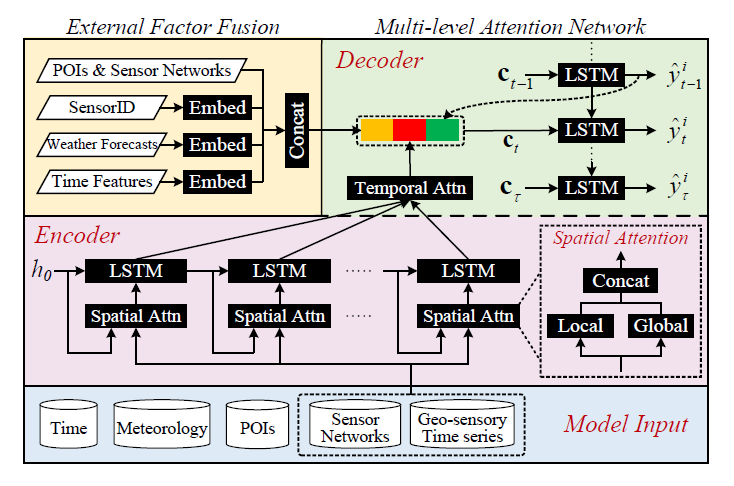
由于是处理的是输入与输出都不定长的时间序列,模型采用的是经典的seq2seq架构,其中Encoder具有两种类型的attention机制(Local与Global),Decoder也具有一种attention机制。值得注意的是,作者在Decoder生成预测阶段又十分巧妙地融合了诸如传感器对应的兴趣点(POI)信息、传感器ID和天气预报数据等外部因素,这种处理方式提高了模型的预测表现。
Encoder中“Spatial Attn”结构内的Local指的是当前传感器的先前数据与空间信息(如传感器网络),Global则指的是其他传感器的数据。Decoder中使用了attention机制自适应地选择用来做预测的时序间隔。
图片左上部分外部因融合模块的输出将作为Decoder阶段输入的一部分。
Local Spatial Attention
给定第$i$个传感器的第$k$维local特征向量$x^(i,k)$,使用attention机制来自适应的获取目标序列与每个local特征之间的动态关联性。
$$
e_t^k=V_l^T tanh(W_l[h_{t-1};S_{t-1}]+U_lx^{i,k}+b_l)
$$
$$
\alpha_t^k=\frac{exp(e_t^k)}{\sum_{j=1}^{N_l}exp(e_t^j)}
$$
其中$v_l ,b_l \in R^T ,W_l \in R^(T*2m) ,U_l \in R^(T*T)$是需要学习的参数。$\alpha^k_t$为特征向量的attention权重,由encoder阶段中输入的特征向量与历史状态决定(如$h_(t-1),s_(t-1)$),这个权重衡量了传感器内部收集的不同特征的重要性高低。
接着,就可以计算Local Spatial Attention的输出向量了,其中$x_t^{i,1}$代表第$i$个传感器在第$t$时刻的第$1$维特征取值。
$$
x_t^{local}=(\alpha_t^{1}x_t^{i,1},\alpha_t^{2}x_t^{i,2}....\alpha_t^{N_l}x_t^{i,N_l})
$$
Global Spatial Attention
这个attention机制是建立在各个传感器之间的时空序列数据都互有关联的前提上。直接使用全部传感器数据序列会导致计算花费过高、降低模型表现,因为可能存在许多不相关联的序列,所以在这个阶段需要先算出各个传感器之间的关联性。
$$
g_t^l=v_g^Ttanh(W_g[h_{t-1};s_{t-1}]+U_gy^l+W^{'}_gX^lu_g+b_g])
$$
其中$v_g,u_g,b_g \in R^T, W_g \in R^{T*2m}, U_g \in R^{T*T}, W_g^{'} \in R^{T*N_l}$是需要学习的参数,这种attention机制可以自适应地选择合适的的相关传感器数据序列。attention权重的计算方式如下。
$$
\beta_t^l=\frac{exp((1-\lambda)g_t^l+\lambda P_{i,l})}{\sum_{j=1}^{N_g}exp((1-\lambda)g_t^l+\lambda P_{i,j})}
$$
其中$P_{i,l}$用于衡量传感器$i,l$之间的地理关联性,如地理距离的倒数。$\lambda$则是可调的超参,如果$\lambda$很大这一项将会使attention权重变得类似于计算地理位置相似性。作者还指出,当$N_g$很大时,可以用与目标传感器距离最近的前$k$个传感器作为近似代替。
接着,就可以计算Global Spatial Attention的输出向量了
$$
x_t^{global}=(\beta_t^1y_t^1,\beta_t^2y_t^2....\beta_t^{N_g}y_t^{N_g})
$$
Temporal Attention
Cho等人在On the properties of neural machine translation: Encoder-decoder approaches一文指出Encoder-Decoder结构的性能会随着Encoder长度的增长而迅速下降,所以需要在Decoder中也需要引入attention机制来解决这个问题。attention机制可以使Decoder自适应地选取Encoder中的应着重关注隐藏层状态。Decoder中t时刻的attention权重计算如下。
$$
u_t^o=v_d^T tanh(W_d^{'} [d_{t-1};s^{'}_{t-1}]+W_dh_o+b_d)
$$
$$
\lambda_t^o=\frac{exp(u_t^o)}{\sum_{j=1}^T exp(u_t^j)}
$$
$$
c_t=\sum_{o=1}^T\lambda_t^oh_o
$$
其中$W_d \in R^{m*m} , W_d^{'} \in R^{m*2n} , v_d,b_d \in R^{m}$是需要学习的参数。
External Factor Fusion
这一步是在Decoder中融合外部因素,这些因素包括time features, meteorological features, SensorID, POIs&Sensor networks,需要注意的是这些外部因素中的大部分都是离散的,所以作者将这些特征映射为低维向量分别送入不同的embedding层中。作者还使用了POIs密度作为POIs的特征,Sensor networks采用的是比较简单的传感器网络结构特征(例如十字路口数量与邻近传感器数量)。由于未来的天气信息难以获取,所以作者采用的是天气预报信息。
Encoder-decoder & Model Training
对于$t$时刻,Encoder的输入为
$$
x_t=[x_t^{local};x_t^{global}]
$$
并采用
$$
h_t=f_e(h_{t-1},x_t)
$$
的方式更新隐藏状态,其中$f_e$表示LSTM unit。
在Decoder阶段,用的是另外一种计算公式
$$
d_t=f_d(d_{t-1},[y_{t-1}^i;c_t;ex_t])
$$
来更新Decoder的隐藏状态,其中$ex_t$就是前面融合的外部因素特征向量,$y_(t-1)^i$是$t-1$时刻的输出值,即对$t-1$时刻的预测值,其计算公式如下。
$$
y_t^i=v_y^T(W_m [c_t;d_t]+b_m)+b_y
$$
其中$W_m \in R^{n*(n+m)},b_m \in R_n,v_y \in R^n, b_y \in R$是需要学习的参数。
最后,采用反向传播算法训练网络,Optimizer采用的是Adam,由于是回归问题,loss函数当然用的是最常见的均方误差$||y_i-y_i^{true}||_2^2$了。
实验结果
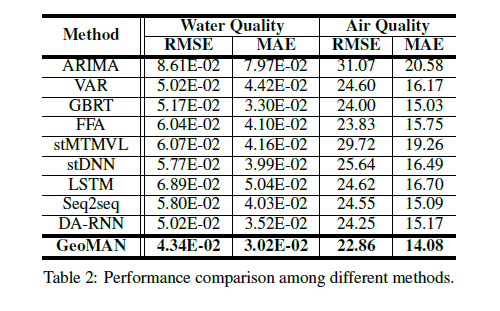
作者采用了两个数据集,分别是中国东南某城市的管网水质和北京市空气质量。结果表明,GeoMAN在RMSE与MAE上表现都优于其他9种模型。
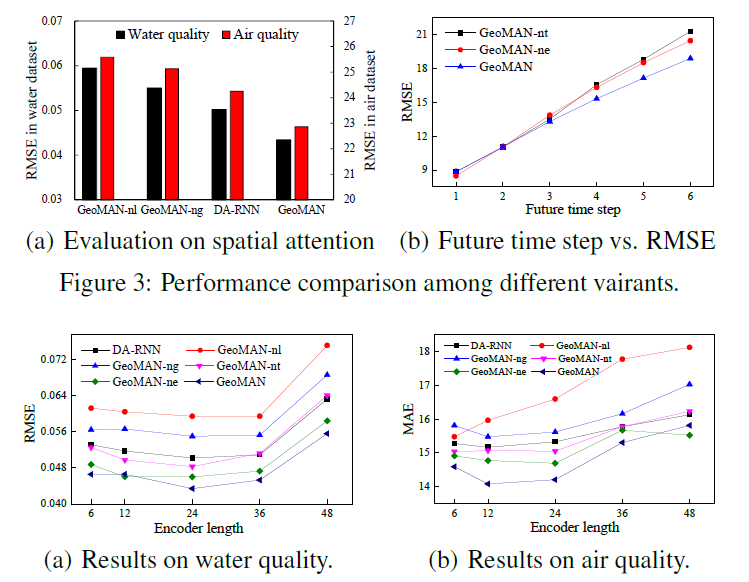
作者还比较了不同Encoder长度下的模型表现,用于验证attention机制的有效性。结果表明当$T=24$时模型在水质数据集下的RMSE最小,当$T$增大时模型的表现也随之快速下降。
不同于水质测试集,当$T=12$时模型在空气质量数据集上RMSE最小,显示出空气质量数据集中并没有在水质测试集中那么长的时间依赖性。
在图3(b)中显示,去掉了attention机制的GeoMAN-nt模型与去掉了融合外部因素的GeoMAN-ne模型表现都有所下降,换句话说,这两种方式都提高了模型的性能。
未来工作
作者将会继续扩展该模型以实现长期的预测,以及探索在现实世界中有限的传感器数量下,实现高精度的地理传感器时间序列预测。