一致性哈希算法原理及Java实现

前言

一致性哈希算法在 1997 年由 MIT 的 Karger 等人在解决分布式 Cache 中而发表的一篇 paper “Consistent Hashing and Random Trees: Distributed Caching Protocols for Relieving Hot Spots on the World Wide Web” 中提出，设计目标是为了解决分布式缓存热点（Hot spot）问题。

这篇 paper 提出在动态变化的 Cache 环境中，哈希算法应该满足的4个适应条件：Balance（均衡）、Monotonicity（单调性）、Spread（分散性）、Load（负载）。

一致性哈希算法可应用于负载均衡、分布式缓存等场景中。以分布式缓存为例，对于 $n$ 台缓存服务器（$n$ 个 node），普通哈希是对资源 $o$ 的请求使用 $ {{\mbox{hash}}(o) \ \% \ n} $ 来映射到某个 node上。这种方式强依赖于 node 的数量，所以当 node 增加或减少时就需要对大量资源进行 rehash。

使用一致性哈希算法，可以很好地解决这个问题，它能够尽可能小的改变 node 和已存在 key 的映射关系。

一致性哈希算法

一致性哈希算法通常借助一个被称为哈希环的整数环来实现，哈希环的值空间为 $ 2^{32} $ ，即 $ 0 \sim 2^{32}-1 $，其中 Node 按顺时针方向分布于哈希环上。对于每个资源（比如 IP 地址），可以通过 $ { {\mbox{hash}}(o) \ \% \ 2^{32}} $ 来映射到哈希环上，每个资源分得处于自己前方顺时针方向的 Node。

例如下图，IP 1 分给 Node A， IP2 与 IP3 分给 Node B，以此类推。

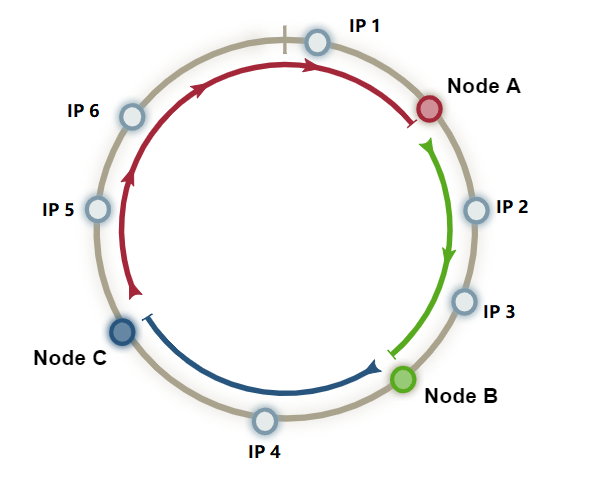
增加节点

如果此时需要需要增加一个 Node D，则需要对处于 Node C 与 Node D 之间的节点进行 rehash，其他 Node B 与 Node C 负责的资源不受影响。

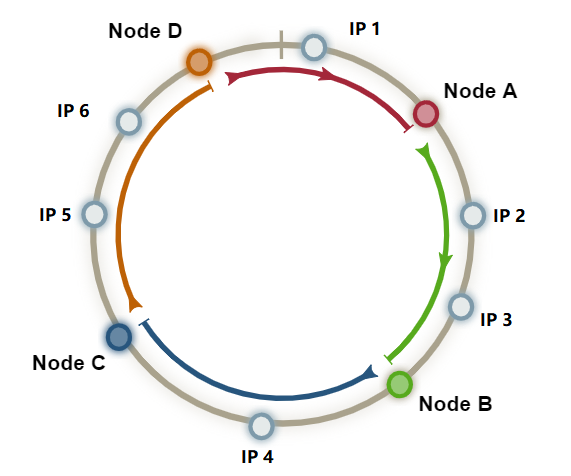
删除节点

假如此时需要删除 Node D，则只需要将处于 Node C 与 Node D 之间的节点进行 rehash 从而映射到 Node A 上即可，此时影响的节点仅有一部分而不是普通哈希中的那么多。

综上，一致性哈希算法对于节点的增减都只需重定位环空间中的一小部分数据，具有较好的容错性和可扩展性。

时间复杂度

N nodes (or slots) and K keys(from ConsistentHashing’s wikipedia)：

	Classic hash table	Consistent hashing
add a node	$O(K)$	$O(K/N + log(N))$
remove a node	$O(K)$	$O(K/N + log(N))$
add a key	$O(1)$	$O(log(N))$
remove a key	$O(1)$	$O(log(N))$

Hash 倾斜问题

Hash 算法的一个考量指标是平衡性，平衡性指的是我们希望每个资源落在任意一个 Node 上的机会都尽可能接近，即下图左边的理想情况，但实际中的情况往往是右边所示。

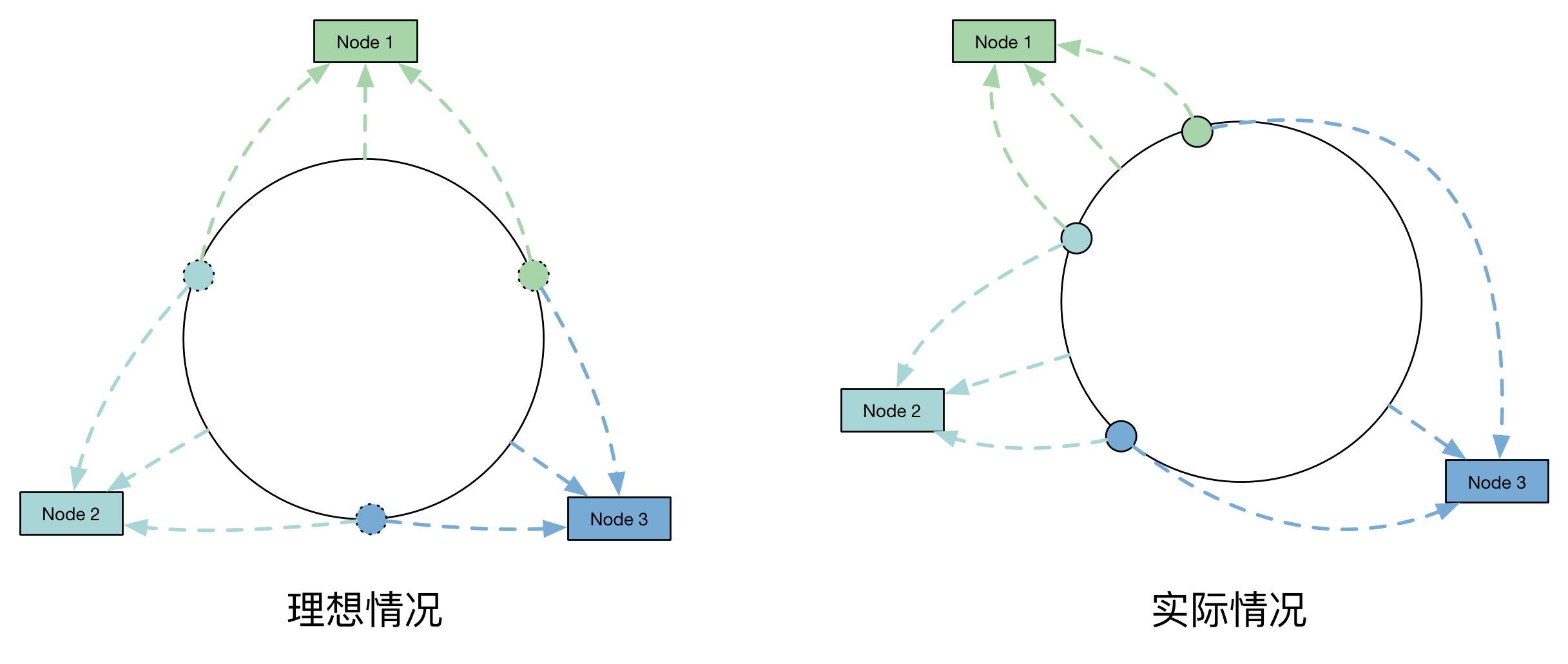
此时的大部分资源都分给了 Node 3，在真实环境中会导致大部分请求都落在了该台服务器上，这就是 Hash 倾斜问题。为了解决这个问题，我们引入虚拟节点。

理论上来说，只要 Node 数量足够大，每个资源在哈希环上就会分散地足够平均，因此我们可以通过加入虚拟节点，每个真实节点负责一部分虚拟节点来提高平衡性。

此时的流程是：资源请求 -> 虚拟节点 -> 真实节点。

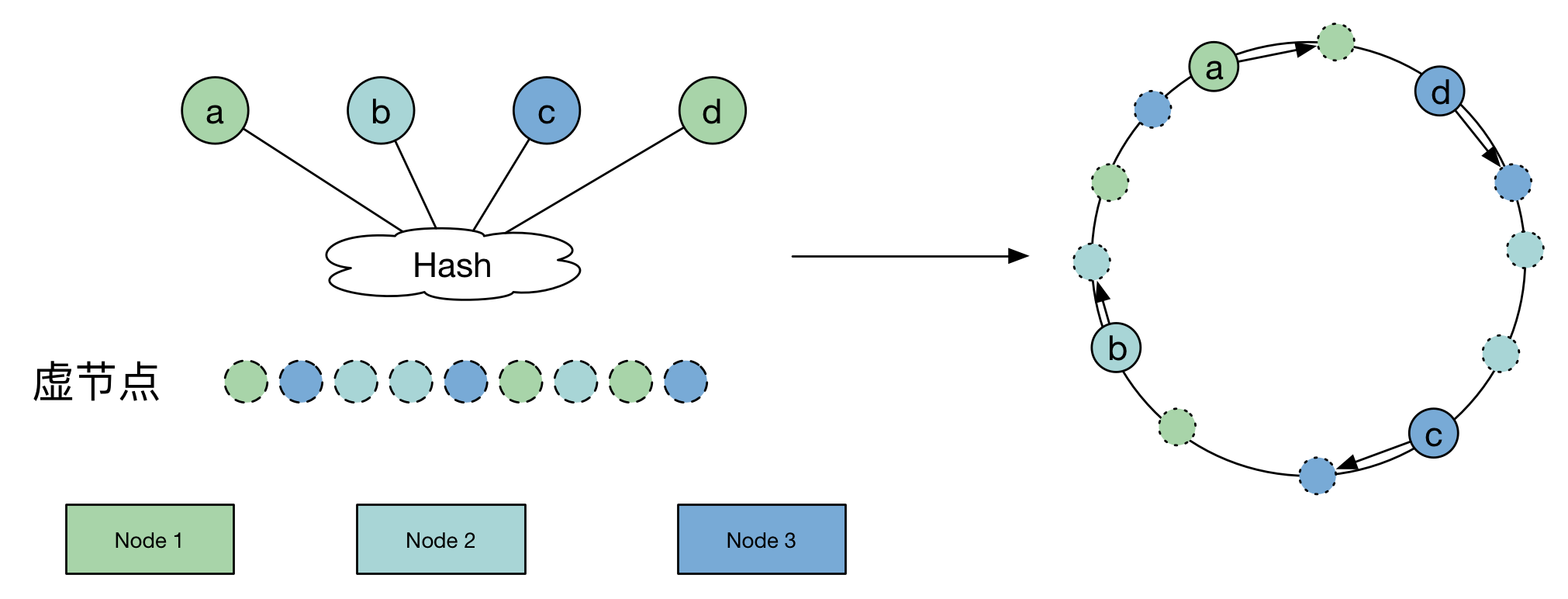
其他哈希算法

Jump Consistent Hash

Google 在 2014 年发表的一篇 paper “A Fast, Minimal Memory, Consistent Hash Algorithm” 中提出了 Jump Consistent Hash。这个算法最早已经在 2011 年加入进 Google Guava 工具库中。

Jump Hash 解决了 Ring Hash 的两个缺点：

零内存消耗。
几乎完美的散列分布。

更多的一致性哈希算法可以参考这篇文章。

一致性哈希算法的 Java 实现

// 定义一个Node节点，包括域名、IP地址和存储数据
public class Node {
    private String domain;
    private String ip;
    private HashMap<String, String> data;
    // ...
}

// 定义一个抽象类Cluster来表示集群
public abstract class Cluster {
    public SortedMap<Integer, Node> nodes;
    // ...
}

// 一致性哈希算法的实现
public class ConsistentHashingCluster extends Cluster {
    // 简单起见这里没用2^32
    private Integer size = 1024;
    // 每个节点有32个虚拟节点
    private Integer virtualNodesNum = 32;

    public ConsistentHashingCluster() {
        super();
    }

    @Override
    public void addNode(Node node) {
        this.nodes.put(node.getIp().hashCode() % size, node);
        for (int i = 0; i < virtualNodesNum; i++) {
            Node newNode = new Node(node.getDomain() + "#vir" + i, node.getIp() + "#vir" + i);
            this.nodes.put(Math.abs((node.getIp() + i).hashCode()) % size, newNode);
        }
    }

    @Override
    public void removeNode(String ip) {
        Node node = this.nodes.get(ip.hashCode() % size);
        this.nodes.remove(ip.hashCode() % size);
        for (int i = 0; i < virtualNodesNum; i++) {
            this.nodes.remove(Math.abs((node.getIp() + i).hashCode()) % size);
        }
    }

    @Override
    public Node get(String ip) {
        return this.nodes.get(ip.hashCode() % size);
    }

    public void putFile(String file) {
        if (null == this.nodes.get(file.hashCode() % size)) {
            Node firstNode = this.nodes.get(nodes.firstKey());
            firstNode.putFile(file);
        } else {
            this.nodes.get(file.hashCode() % size).putFile(file);
        }
    }

    public Node getFileNode(String file) {
        if (null == this.nodes.get(file.hashCode() % size)) {
            return this.nodes.get(nodes.firstKey());
        } else {
            Node tempNode = this.nodes.get(file.hashCode() % size);
            String ip = tempNode.getIp();
            // 如果是虚拟节点
            if (ip.contains("#")) {
                // 找到对应的真实节点
                int i = ip.indexOf("#");
                String realIp = ip.substring(0, i);
                return this.nodes.get(realIp.hashCode() % size);
            } else {
                return this.nodes.get(ip.hashCode() % size);
            }
        }
    }
}