深入理解Redis Zset原理

前言

最近把 AirNet 中的空气质量排行换成了用 Zset 实现，这篇笔记就来深入了解下 Zset 的底层实现原理。

Zset 编码的选择

zset

在通过 ZADD 命令添加第一个元素到空 key 时， Redis 会通过检查输入的第一个元素来决定使用何种编码。

如果第一个元素符合以下条件的话，就创建一个 REDIS_ENCODING_ZIPLIST 编码的 Zset：

服务器属性 server.zset_max_ziplist_entries 的值大于 0 （默认为 128 ）。
元素的 member 长度小于服务器属性 server.zset_max_ziplist_value 的值（默认为 64 ）。

否则，创建一个 REDIS_ENCODING_SKIPLIST 编码的 Zset。

对于一个 REDIS_ENCODING_ZIPLIST 编码的 Zset，只要满足以下任一条件，则会被转换为 REDIS_ENCODING_SKIPLIST 编码：

ziplist 所保存的元素数量超过服务器属性 server.zset_max_ziplist_entries 的值（默认值为 128 ）
新添加元素的 member 的长度大于服务器属性 server.zset_max_ziplist_value 的值（默认值为 64 ）

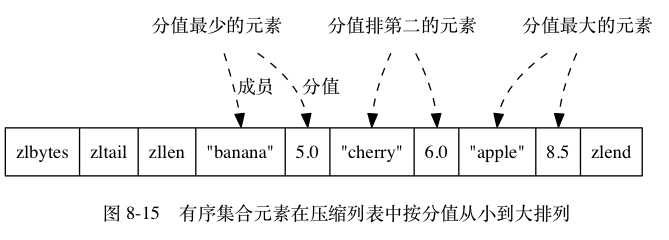
ziplist 编码的 Zset 使用紧挨在一起的压缩列表节点来保存，第一个节点保存 member，第二个保存 score。ziplist 内的集合元素按 score 从小到大排序，其实质是一个双向链表。虽然元素是按 score 有序排序的，但对 ziplist 的节点指针只能线性地移动，所以在 REDIS_ENCODING_ZIPLIST 编码的 Zset 中，查找某个给定元素的复杂度为 $O(N)$。

ziplist

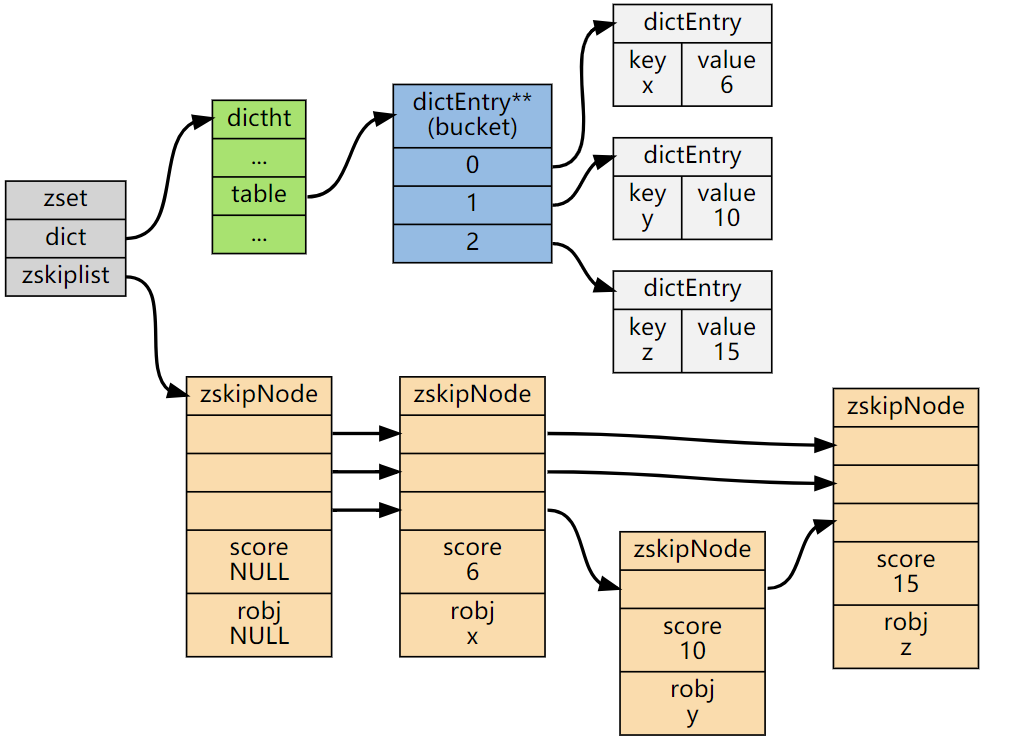
skiplist 编码的 Zset 底层为一个被称为 zset 的结构体，这个结构体中包含一个字典和一个跳跃表。跳跃表按 score 从小到大保存所有集合元素，查找时间复杂度为平均 $O(logN)$，最坏 $O(N)$ 。字典则保存着从 member 到 score 的映射，这样就可以用 $O(1)$ 的复杂度来查找 member 对应的 score 值。虽然同时使用两种结构，但它们会通过指针来共享相同元素的 member 和 score，因此不会浪费额外的内存。

/* zset结构体 */
typedef struct zset {
    // 字典，维护元素值和分值的映射关系
    dict *dict;
    // 按分值对元素值排序序，支持O(logN)数量级的查找操作
    zskiplist *zsl;
} zset;

skiplist

Skiplist 跳跃表

跳表由 William Pugh 于1990年发表的论文 Skip lists: a probabilistic alternative to balanced trees 中被首次提出，查找时间复杂度为平均 $O(logN)$，最差 $O(N)$，在大部分情况下效率可与平衡树相媲美，但实现比平衡树简单的多，跳表是一种典型的以空间换时间的数据结构。

跳表具有以下几个特点：

由许多层结构组成。
每一层都是一个有序的链表。
最底层 (Level 1) 的链表包含所有元素。
如果一个元素出现在 Level i 的链表中，则它在 Level i 之下的链表也都会出现。
每个节点包含两个指针，一个指向同一链表中的下一个元素，一个指向下面一层的元素。

跳表的查找会从顶层链表的头部元素开始，然后遍历该链表，直到找到元素大于或等于目标元素的节点，如果当前元素正好等于目标，那么就直接返回它。如果当前元素小于目标元素，那么就垂直下降到下一层继续搜索，如果当前元素大于目标或到达链表尾部，则移动到前一个节点的位置，然后垂直下降到下一层。正因为 Skiplist 的搜索过程会不断地从一层跳跃到下一层的，所以被称为跳跃表。

skiplist2

跳表的作者是这么介绍跳表的：

“Skip lists are a probabilistic data structure that seem likely to supplant balanced trees as the implementation method of choice for many applications. Skip list algorithms have the same asymptotic expected time bounds as balanced trees and are simpler, faster and use less space.”

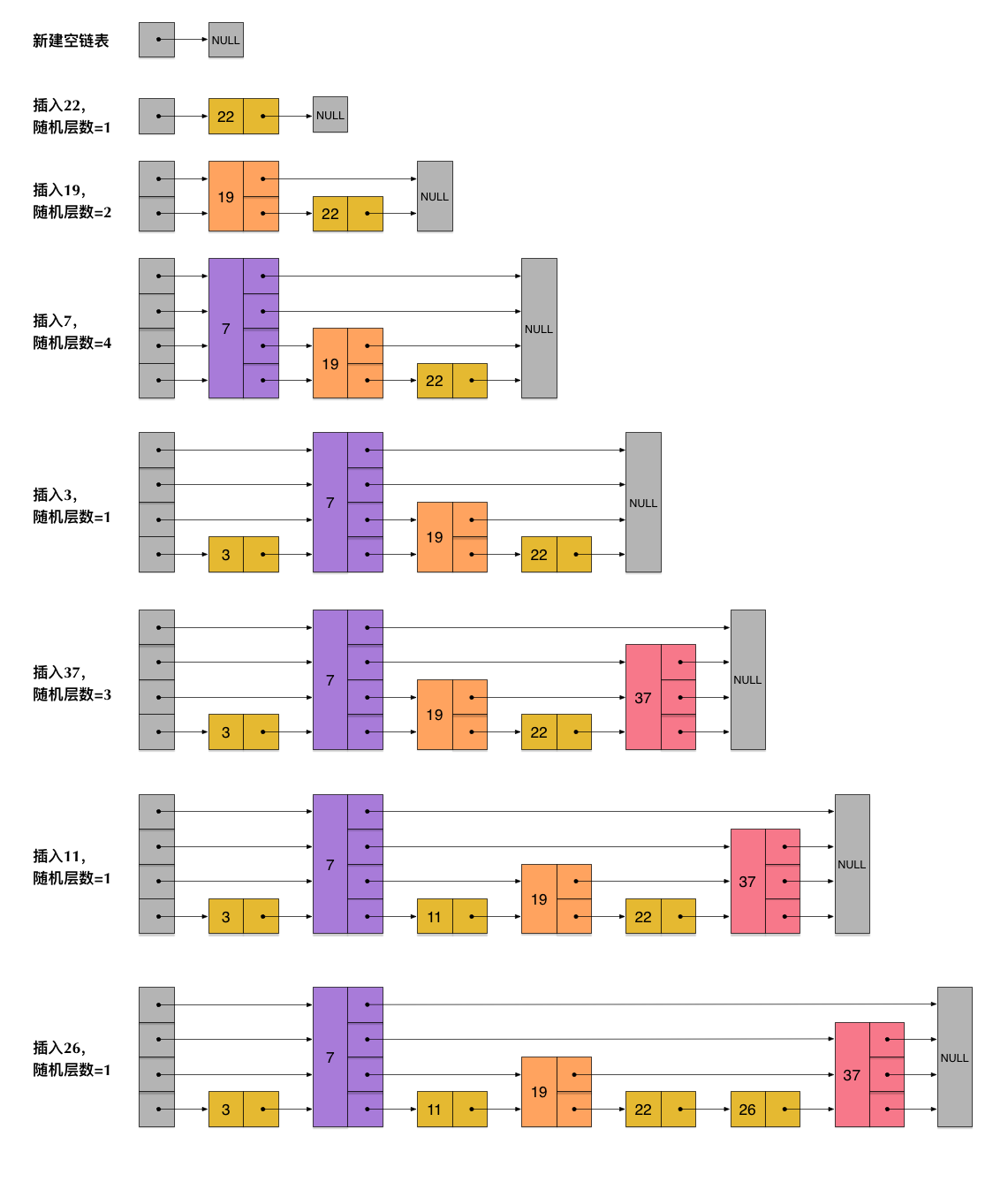
跳表是一个“概率型”的数据结构，这一句话十分有意思，指的就是跳表在插入操作时，元素的插入层数完全是随机指定的。实际上该决定插入层数的随机函数对跳表的查找性能有着很大影响，这并不是一个普通的服从均匀分布的随机数，它的计算过程如下：

指定一个节点最大的层数 MaxLevel，指定一个概率 p，层数 lvl 默认为 1 。
生成一个 0~1 的随机数 r，若 r < p，且 lvl < MaxLevel ，则执行 lvl ++。
重复第 2 步，直至生成的 r > p 为止，此时的 lvl 就是要插入的层数。

伪函数如下：

randomLevel()
    lvl := 1
    -- random() that returns a random value in [0...1)
    while random() < p and lvl < MaxLevel do
        lvl := lvl + 1
    return lvl

在 Redis 的 skiplist 实现中，$p = 1/4$ ，$MaxLevel = 32$。

Redis中的 Skiplist 与经典 Skiplist 相比，有如下不同：

分数(score)允许重复，即 Skiplist 的 key 允许重复，经典 Skiplist 中是不允许的。
在比较时，不仅比较分数（相当于 Skiplist 的 key），还比较数据本身。在 Redis 的 Skiplist 实现中，数据本身的内容唯一标识这份数据，而不是由 key 来唯一标识。另外，当多个元素分数相同的时候，还需要根据数据内容来进字典排序。
第 1 层链表不是一个单向链表，而是一个双向链表。这是为了方便以倒序方式获取一个范围内的元素。

此外，JDK 提供了以下两种跳表实现：

ConcurrentSkipListMap：在功能上类似 HashMap。
ConcurrentSkipListSet ：在功能上类似 HashSet。

Skiplist与平衡树、哈希表的比较

Skiplist 和各种平衡树（如AVL、红黑树等）的元素是有序排列的，而哈希表不是有序的。因此，在哈希表上只能做单个 key 的查找，不适宜做范围查找。
在做范围查找的时候，平衡树比 Skiplist 操作要复杂。在平衡树上，我们找到指定范围的小值之后，还需要以中序遍历的顺序继续寻找其它不超过大值的节点。如果不对平衡树进行一定的改造，这里的中序遍历并不容易实现。而在skiplist上进行范围查找就非常简单，只需要在找到小值之后，对第 1 层链表进行若干步的遍历就可以实现。
平衡树的插入和删除操作可能引发子树的调整，逻辑复杂，而 Skiplist 的插入和删除只需要修改相邻节点的指针，操作简单又快速。
从内存占用上来说，Skiplist 比平衡树更灵活一些。一般来说，平衡树每个节点包含 2 个指针（分别指向左右子树），而 Skiplist 每个节点包含的指针数目平均为$1/(1-p)$，具体取决于参数 $p$ 的大小。如果像 Redis 里的实现一样，取 $p=1/4$，那么平均每个节点包含 1.33 个指针，比平衡树更有优势。
查找单个 key，Skiplist 和平衡树的时间复杂度都为 $O(logN)$；而哈希表在保持较低的哈希值冲突概率的前提下，查找时间复杂度接近 $O(1)$，性能更高一些。
从算法实现难度上来比较，Skiplist 比平衡树要简单得多。

Redis Zset 采用跳表而不是平衡树的原因

Redis Zset 作者是这么解释的：

There are a few reasons:
1) They are not very memory intensive. It’s up to you basically. Changing parameters about the probability of a node to have a given number of levels will make then less memory intensive than btrees.
1) 也不是非常耗费内存，实际上取决于生成层数函数里的概率 p，取决得当的话其实和平衡树差不多。

2) A sorted set is often target of many ZRANGE or ZREVRANGE operations, that is, traversing the skip list as a linked list. With this operation the cache locality of skip lists is at least as good as with other kind of balanced trees.
2) 因为有序集合经常会进行 ZRANGE 或 ZREVRANGE 这样的范围查找操作，跳表里面的双向链表可以十分方便地进行这类操作。

3) They are simpler to implement, debug, and so forth. For instance thanks to the skip list simplicity I received a patch (already in Redis master) with augmented skip lists implementing ZRANK in O(log(N)). It required little changes to the code.
3) 实现简单，ZRANK 操作还能达到 $O(logN)$ 的时间复杂度。